Ένα σύστημα σωμάτων και η τριβή.

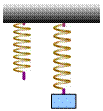
Δίνεται το σύστημα των σωμάτων Α, Β και Σ, όπου το σώμαΑ, μάζας Μ=1,5kg, συνδέεται με αβαρές νήμα, μέσω αβαρούς τροχαλίας με το σώμα Σ, μάζας m=0,5kg. Τα σώματα ηρεμούν.

i)   Να αποδείξτε ότι το σώμα Α δεν δέχεται δύναμη τριβής από το σώμα Β.

ii)  Να βρεθεί το μέτρο της τριβής που ασκείται στο Α σώμα από το τραπέζι.

iii) Σε μια στιγμή αφαιρούμε το σώμα Β, οπότε το σώμα Σ πέφτει και φτάνει στο έδαφος με ταχύτητα υ₁=0,8m/s, όπου και σταματά. Αν αρχικά το Σ βρισκόταν σε ύψος h=0,32m από το έδαφος, να βρεθούν:

α) Ο συντελεστής τριβής ολίσθησης μεταξύ του σώματος Α και του τραπεζιού.

β) Η συνολική απόσταση που διανύει το Α σώμα πάνω στο τραπέζι μέχρι να σταματήσει.

Δίνεται g=10m/s².

Απάντηση:

ή

Ένα σύστημα σωμάτων και η τριβή.

Ένα σύστημα σωμάτων και η τριβή.

Ερωτήσεις στις τριβές.

Πιέζοντας ένα κουτί με το δάκτυλό μας το κρατάμε σε επαφή με έναν κατακόρυφο τοίχο, ασκώντας του οριζόντια δύναμη F, όπως στο σχήμα.

i)  Να σχεδιάστε τις δυνάμεις που ασκούνται στο κουτί.

ii) Αν πιέσουμε λιγότερο το κουτί, μειώνοντας την δύναμη F που ασκούμε, το κουτί πέφτει. Μπορείτε να το ερμηνεύσετε;

Δείτε όλες τις ερωτήσεις με κλικ εδώ.

Κίνηση σε κεκλιμένο επίπεδο. Ένα test.

Το σώμα Α του σχήματος, μάζας m=2kg, αφήνεται σε ένα σημείο λείου κεκλιμένου επιπέδου, από κάποιο ύψος h.

 Δίνεται η κλίση του επιπέδου θ=30° (ημθ= ½, συνθ=√3/2   και g=10m/s².

i)  Να υπολογίστε το βάρος του σώματος Α.

ii) Να σχεδιάστε στο σχήμα τις δυνάμεις που ασκούνται στο σώμα Α.

iii) Να αναλύσετε το βάρος και να βρείτε τις συνιστώσες του πάνω στους άξονες x και y που φαίνονται στο σχήμα.

iv) Να βρείτε (διεύθυνση φορά και μέτρο) τη δύναμη που ασκεί το σώμα Α στο κεκλιμένο επίπεδο.

v) Να υπολογίστε την επιτάχυνση του σώματος και την απόσταση που θα διανύσει σε χρονικό διάστημα 4s.

vi) Αν από το ίδιο ύψος ενός όμοιου κεκλιμένου επιπέδου, ταυτόχρονα με το σώμα Α, αφεθεί το σώμα Γ, μικρότερης μάζας, τότε:

α) Το σώμα Γ θα αποκτούσε μικρότερη επιτάχυνση

β) Πρώτο στη βάση του επιπέδου θα έφτανε το Α σώμα.

γ) Το  Γ θα ασκούσε μικρότερη δύναμη στο επίπεδο.

δ) Η κίνηση του σώματος Γ θα ήταν ευθύγραμμη ομαλή.

Χαρακτηρίστε τις παραπάνω προτάσεις ως σωστές ή λανθασμένες.

Μονάδες 2+1+4+3+6+4=20

Και σύντομες απαντήσεις  απαντήσεις.

Θα ανασηκωθεί το σώμα;

Ή προσπαθώντας να διδάξουμε σύμφωνα με τις οδηγίες…

-------------------------------------

Ένα σώμα μάζας 1kg ηρεμεί σε λείο οριζόντιο επίπεδο. Σε μια στιγμή ασκούμε πάνω του μια  δύναμη μέτρου 14Ν, η διεύθυνση της οποίας μπορεί να είναι όπως φαίνεται στα παρακάτω σχήματα.

i)  Στην περίπτωση του (α) σχήματος, πόση επιτάχυνση θα αποκτήσει το σώμα;

ii) Το σώμα στο (β)  σχήμα, όπου θ=30°:

α) θα κινηθεί οριζόντια  

β) θα κινηθεί στη διεύθυνση της δύναμης F,   

γ) θα κινηθεί σε άλλη διεύθυνση.

iii) Να υπολογιστεί η επιτάχυνση του σώματος στην περίπτωση του (β) σχήματος.

iv) Αν η δύναμη στο (γ) σχήμα σχηματίζει γωνία φ=60° με την οριζόντια  διεύθυνση, τότε το σώμα:

α) θα κινηθεί οριζόντια   ,

β) θα κινηθεί στη διεύθυνση της δύναμης F,   

γ) θα κινηθεί σε άλλη διεύθυνση.

Δίνεται g=10m/s².

Απάντηση:

Η απόσταση των σωμάτων μετά το κόψιμο του νήματος.

Σε λείο οριζόντιο επίπεδο ηρεμούν δυο σώματα Α και Β με μάζες m₁=1kg και m₂=3kg αντίστοιχα, δεμένα στα άκρα ενός οριζόντιου νήματος μήκους ℓ=1m, όπως φαίνεται στο σχήμα.

Κάποια στιγμή ασκούμε στο σώμα Β μια οριζόντια δύναμη μέτρου F=12Ν και τα σώματα κινούνται προς τα δεξιά.

i)  Να βρεθεί η τάση του νήματος.

ii) Σε μια στιγμή το νήμα που συνδέει τα δυο σώματα κόβεται. Ποια η απόσταση των δύο σωμάτων  2s  μετά τη στιγμή που κόπηκε το νήμα;

Απάντηση:

Αντίσταση του αέρα και πτώση σώματος.

Αφήνουμε ένα σώμα ελεύθερο να πέσει από ορισμένο ύψος και στο διπλανό διάγραμμα δίνεται η ταχύτητά του σε συνάρτηση με το χρόνο.

i) Η κίνηση του σώματος είναι ελεύθερη πτώση.

ii) Στο σώμα ασκείται η αντίσταση του αέρα, μια σταθερή δύναμη αντίθετη της ταχύτητας.

iii) Τη χρονική στιγμή t₃ η αντίσταση του αέρα έχει το ίδιο μέτρο με το βάρος.

Να χαρακτηρίσετε τις παραπάνω προτάσεις ως σωστές ή λανθασμένες, δικαιολογώντας την άποψή σας.

Απάντηση:

Κίνηση σώματος με δύναμη που μεταβάλλεται.

  

Ένα σώμα ηρεμεί σε λείο οριζόντιο επίπεδο, στο σημείο Ο. Σε μια στιγμή t₀=0 δέχεται την επίδραση οριζόντιας δύναμης, η τιμή της οποίας μεταβάλλεται όπως στο διάγραμμα

Ποιες προτάσεις είναι σωστές και ποιες λάθος:

i) Από 0-t₁ το σώμα κινείται και η κίνησή του είναι ευθύγραμμη ομαλά επιταχυνόμενη.

ii) Στο χρονικό διάστημα t₁-2t₁ το σώμα ηρεμεί.

iii) Στο χρονικό διάστημα 2t₁-3t1 το σώμα κινείται επιταχυνόμενο προς τα αριστερά.

iv) Τη στιγμή  3t₁ το σώμα απέχει μεγαλύτερη απόσταση από την αρχική θέση Ο, από ότι τη στιγμή 2t₁.

v) Τη στιγμή  3t₁ το σώμα έχει ταχύτητα προς τα δεξιά.

Να δικαιολογήσετε τις απαντήσεις σας.

Απάντηση:

Ένα test δυναμικής.

Ένα σώμα μάζας 2kg ηρεμεί, όπως στο  σχήμα, στο κάτω άκρο ενός κατακόρυφου ελατηρίου, προκαλώντας του επιμήκυνση Δℓ=0,4m.

i)  Να σχεδιάστε τις δυνάμεις που ασκούνται στο σώμα και να υπολογίστε τα μέτρα τους, δικαιολογώντας ΑΝΑΛΥΤΙΚΑ το τι κάνετε.

ii) Να υπολογίστε την σταθερά του ελατηρίου.

iii) Πιάνουμε το σώμα με το χέρι μας και το μετακινούμε κατακόρυφα προς τα κάτω κατά 0,2m. Σε μια στιγμή το αφήνουμε ελεύθερο να κινηθεί. Να εξηγείστε γιατί θα κινηθεί προς τα πάνω και να υπολογίστε την αρχική επιτάχυνση που θα αποκτήσει, αμέσως μόλις αφεθεί να κινηθεί.

iv) Η κίνηση του σώματος είναι ευθύγραμμη ομαλά επιταχυνόμενη ή όχι; Να εξηγείστε ΑΝΑΛΥΤΙΚΑ την άποψή σας.

Δίνεται η επιτάχυνση της βαρύτητας g=10m/s².

Απάντηση

Κίνηση σε λείο επίπεδο με την επίδραση δύο δυνάμεων.

Ένα σώ­μα μά­ζας 2kg κι­νεί­ται σε λεί­ο  ο­ρι­ζό­ντιο ε­πί­πε­δο, με την ε­πί­δρα­ση 2 ο­ρι­ζο­ντί­ων δυ­νά­με­ων F₁=4N προς τα δε­ξιά και F₂ =10Ν προς τ' α­ρι­στε­ρά. Σε μια στιγ­μή t₀=0 έ­χει τα­χύ­τη­τα υ₀=12m/s προς τα δε­ξιά.

i) Ποια πρόταση είναι σωστή:       

α) Η επιτάχυνση του σώματος είναι προς τα δεξιά.    

β) Το σώμα θα κινηθεί αμέσως προς τ’ αριστερά.      

γ) Ο ρυθμός μεταβολής της ταχύτητας έχει μέτρο 3m/s/s.   

δ) Η αδράνεια του σώματος θα μικρύνει αν καταργηθεί η δύναμη F₂.

ii) Η  τα­χύ­τη­τά του τη στιγμή t₁=2s είναι:          

α. 2 m/s .              β. 6 m/s.              γ. 8 m/s.       δ. 12 m/s.

iii)  Αν τη στιγμή t₁=2s στα­μα­τά να α­σκεί­ται η δύ­να­μη F₁, τότε:

α)  Θα αυξηθεί η αδράνεια του σώματος.       

β) Το σώμα θα κινηθεί για λίγο ακόμη και μετά θα σταματήσει.       

γ) Ο ρυθμός μεταβολής της ταχύτητας θα αλλάξει.   

iv)  Να υπολογιστεί η ταχύτητα του σώματος τη στιγμή t₂=6s.

Απάντηση:

Δύναμη και επιτάχυνση

Ένα παιδί εκτοξεύει από κάποιο ύψος, μια μπάλα οριζόντια και στο σχήμα δίνονται τρεις θέσεις της μπάλας, κατά την κίνησή της . 

Να σχεδιάστε τις δυνάμεις που ασκούνται στην μπάλα και την επιτάχυνσή της για τις θέσεις αυτές.

Αντίσταση του αέρα δεν υπάρχει.

Απάντηση:

Δύναμη από ελατήριο και επιτάχυνση.

Ένα σώμα βάρους 40Ν ηρεμεί στο κάτω άκρο ενός κατακόρυφου ελατηρίου, προκαλώντας του επιμήκυνση x₁=0,1m. Δένουμε το σώμα με ένα νήμα και το τραβάμε, με αποτέλεσμα το σώμα να κατέβει χαμηλότερα κατά x₂= 0,2m.

i)   Σχεδιάστε τις δυνάμεις που ασκούνται στο σώμα στις δύο θέσεις του σχήματος.

ii)  Υπολογίστε την σταθερά του ελατηρίου.

iii) Πόση είναι η τάση του νήματος στο δεύτερο σχήμα;

iv) Σε μια στιγμή κόβουμε το νήμα. Να υπολογίστε την επιτάχυνση του σώματος αμέσως μετά το κόψιμο του νήματος.

v) Ποιος ο ρυθμός μεταβολής της ταχύτητας τη στιγμή που το σώμα έχει μετακινηθεί κατά 0,4m προς τα πάνω;

Απάντηση:

Όριο και μείωση ταχύτητας αυτοκινήτου.

Ένα αυτοκίνητο κινείται ευθύγραμμα με ταχύτητα υ₀=108km/h, όταν μπαίνει σε κατοικημένη περιοχή. Τη στιγμή που το αυτοκίνητο περνά δίπλα από την πινακίδα που επιβάλλει όριο ταχύτητας υ₁=36k/h, ο οδηγός φρενάρει με αποτέλεσμα το αυτοκίνητο να αποκτήσει σταθερή επιτάχυνση (επιβράδυνση), οπότε μετά από 4s έχει αποκτήσει την επιθυμητή ταχύτητα, με την οποία συνεχίζει μέχρι την επόμενη πινακίδα, η οποία του επιτρέπει να αυξήσει ξανά την ταχύτητά του. Η απόσταση μεταξύ των δύο πινακίδων είναι 280m.

i)   Να υπολογίσετε την μεταβολή της ταχύτητας στη διάρκεια του φρεναρίσματος.

ii) Να βρεθεί η τιμή της επιτάχυνσης.

iii) Σε πόση απόσταση από την πρώτη πινακίδα το αυτοκίνητο έχει αποκτήσει ταχύτητα 10m/s;

iv) Πόσο χρόνο χρειάστηκε το αυτοκίνητο για να κινηθεί από τη μια πινακίδα μέχρι την άλλη;

v)  Θεωρώντας ότι η πρώτη πινακίδα βρίσκεται στη θέση x₀=0, καθώς και t₀=0 τη στιγμή που περνά δίπλα της το αυτοκίνητο, να κάνετε τις γραφικές παραστάσεις της ταχύτητας και της θέσης του αυτοκινήτου σε συνάρτηση με το χρόνο.

Απάντηση:

Ωριαίο Διαγώνισμα στην Κινηματική

Ο Γιάννης βγαίνει από το σπίτι του για να δώσει ένα βιβλίο στην Αννούλα, που το σπίτι της βρίσκεται σε απόσταση 400m. Κινούμενος με σταθερή ταχύτητα μετά από 100 s (δευτερόλεπτα) φτάνει στο σπίτι του Κώστα, που απέχει 120m από το δικό του. Σταματά για 15s και συμφωνούν να γυρίσει σε λίγο για να παίξουν μαζί. Κατόπιν περπατά, λίγο πιο γρήγορα και μετά από 200s φτάνει στην Αννούλα. Της δίνει το βιβλίο, λένε και «δυο κουβέντες» μέσα σε 35s και μετά τρέχοντας με σταθερή ταχύτητα επιστρέφει στο σπίτι του Κώστα μετά από 70s.

Θεωρείστε ότι ο Γιάννης ξεκίνησε τη στιγμή t_ο=0 και ότι το σπίτι του βρίσκεται στη θέση x_ο=0, ενώ η προς τα δεξιά κατεύθυνση είναι θετική.

Να συμπληρωθούν τα κενά στις παρακάτω προτάσεις:

i)  Ο Γιάννης φτάνει στην Αννούλα τη χρονική στιγμή …… και επιστρέφει  στον Κώστα τη χρονική στιγμή ……….

ii)  Ο Κώστας βρίσκεται στη θέση …………. Ενώ η Αννούλα στη θέση …….

iii) Στα πρώτα 100s ο Γιάννης μετατοπίζεται κατά ………… ενώ κατά την επιστροφή του κατά …………….

iv)  Στην αρχή ο Γιάννης κινήθηκε με ταχύτητα υ₁= …………… Από τον Κώστα μέχρι την Αννούλα με ταχύτητα υ₂=…………………. Ενώ κατά την επιστροφή του με ταχύτητα υ₃=……………….

v) Να υπολογίσετε τη μέση ταχύτητα του Γιάννη για όλη την διάρκεια της κίνησής του.

Δείτε όλο το  διαγώνισμα με σύντομες απαντήσεις από εδώ.

Από εδώ μπορείτε να δείτε 4 παραλλαγές των παραπάνω θεμάτων.

Κινηματική. Ένα test 2011-12

Ένα σώμα κινείται ευθύγραμμα και στο σχήμα δίνεται η ταχύτητά του σε συνάρτηση με το χρόνο.

i)  Η κίνηση από 0-2s είναι …………..…………………………. ενώ από 2s-6s είναι …………….…………………………….

ii)  Ποιες προτάσεις είναι σωστές και ποιες λάθος

α)  Η αρχική ταχύτητα του σώματος είναι 8m/s.

β)  Ο ρυθμός μεταβολής της θέσης είναι σταθερός από 0s-2s.

γ)  Από 2s-6s η επιτάχυνση έχει την κατεύθυνση της ταχύτητας

δ) Από 2s-6s η επιτάχυνση έχει την κατεύθυνση της μεταβολής της ταχύτητας.

ε) Από 0-2s η ταχύτητα έχει την κατεύθυνση της μεταβολής της θέσης.

ii) Να βρεθεί η μετατόπισή του από 0-6s.

iii)  Να βρεθεί η επιτάχυνσή του στο χρονικό διάστημα από 2s-6s.

iv)  Ποια χρονική στιγμή το σώμα έχει ταχύτητα υ₁=5,2m/s;

v) Πόση είναι η μετατόπιση του σώματος από 0-2,5s;

Μονάδες 2+5+3+3+3+4=20

Απαντήσεις

ΕΟΜΚ. Ένα test. 11-12

Ένα σώμα κινείται ευθύγραμμα και στο σχήμα δίνεται η ταχύτητά του σε συνάρτηση με το χρόνο.

i)  Ποιες προτάσεις είναι σωστές και ποιες λάθος

α)  Η αρχική ταχύτητα του σώματος είναι 2m/s.

β)  Στο χρονικό διάστημα από 2s-4s το σώμα δεν κινείται.

γ)  Από 0-2s η επιτάχυνση αυξάνεται, ενώ από 4s-6s μειώνεται.

ii)  Να κάνετε τις αντιστοιχίσεις

iii) Να υπολογίστε την επιτάχυνση του σώματος, όπου υπάρχει.

iv) Να βρεθεί η μετατόπιση του σώματος μέχρι τη στιγμή t₂=0,6s και η ταχύτητά του τη χρονική στιγμή t₁=5,2s.

Μονάδες 6+3+4+(4+3)=20

  Απαντήσεις.

Απόσταση ασφαλείας μεταξύ αυτοκινήτων.

Σε ένα ευθύγραμμο δρόμο κινούνται με την ίδια ταχύτητα υ₀=72km/h δύο φορτηγά σε απόσταση d μεταξύ τους όπως στο σχήμα.

Σε μια στιγμή ο οδηγός του Α φορτηγού βλέπει ένα εμπόδιο και φρενάρει απότομα. Ο χρόνος αντίδρασής του είναι t₁=0,8s. Τον ίδιο χρόνο αντίδρασης έχει και ο οδηγός του Β φορτηγού που βλέπει τα πίσω φανάρια του φορτηγού που προπορεύεται. Τα δύο φορτηγά επιβραδύνονται με την ίδια επιβράδυνση και τελικά σταματούν σε επαφή του πίσω προφυλακτήρα του Α με τον μπροστινό του Β.

Να υπολογιστεί η αρχική απόσταση d, μεταξύ των δύο φορτηγών.

Απάντηση:

ή

Απόσταση ασφαλείας μεταξύ αυτοκινήτων.

Απόσταση ασφαλείας μεταξύ αυτοκινήτων.

Θέση-μετατόπιση-ταχύτητα στην ΕΟΚ. Άλλο ένα test.

Κατά μήκος ενός ευθύγραμμου δρόμου περπατά ένα παιδί και στο σχήμα φαίνονται οι θέσεις του. Το παιδί ξεκινά για t=0 από τη θέση x=0 (σημείο Ο). Μετά από 40 δευτερόλεπτα, φτάνει στο σημείο Α. Στη συνέχεια χρειάζεται 20 δευτερόλεπτα για να πάει  στο Β, όπου και σταματά για 10  δευτερόλεπτα και επιστρέφει στο σημείο Γ περπατώντας για 10 δευτερόλεπτα ακόμη.

i)   Να συμπληρωθούν τα κενά στο παρακάτω κείμενο:

Τη χρονική στιγμή t=40s το παιδί βρίσκεται στη θέση …………. ενώ για t=65s στη θέση ……….. Η μετατόπιση του παιδιού από 40s-60s είναι …………….. ενώ από 70s-80s είναι ……………….

ii)  Να  βρεθεί η μέση ταχύτητα του παιδιού από:

α)  Το σημείο Ο μέχρι το Α.

β)  Το σημείο Α μέχρι το Γ.

iii)  Αν το παιδί κινείται με σταθερή ταχύτητα από το Α στο Β, να βρεθεί η ταχύτητά του και η θέση του τη χρονική στιγμή t₁=48s.

iv) Να γίνει το διάγραμμα της θέσης του παιδιού  σε συνάρτηση με το χρόνο (x-t), θεωρώντας ότι κάθε επιμέρους κίνηση πραγματοποιείται με σταθερή ταχύτητα.

Μονάδες 20+30+30+20=100

Θέση-μετατόπιση-ταχύτητα στην ΕΟΚ. Ένα test.

Ένα αυτοκίνητο κινείται σε ευθύγραμμο δρόμο και στο διάγραμμα  δίνεται η θέση του σε συνάρτηση με το χρόνο.

i ) Να συμπληρωθούν τα κενά στο παρακάτω κείμενο:

Τη χρονική στιγμή t=0s το αυτοκίνητο βρίσκεται στη θέση …………. ενώ για t=5s στη θέση ……….. Η μετατόπισή του από 0s-5s είναι …………….. ενώ από 7s-10s είναι ……………….

ii) Να σημειώστε πάνω στο παρακάτω σχήμα τη θέση του αυτοκινήτου τις χρονικές στιγμές t₁=6s και t₂=10s (σημεία Α και Β). Σχεδιάστε επίσης πάνω στο σχήμα τη μετατόπιση του αυτοκινήτου στο παραπάνω χρονικό διάστημα.

iii)  Να  βρεθεί η ταχύτητα του αυτοκινήτου από:

     α)  0-5s.

     β)  7s-10s.

iv) Να βρεθεί η μετατόπιση του αυτοκινήτου από τη στιγμή t₁=7s μέχρι τη στιγμή t₂=8,4s, καθώς και η θέση του τη  στιγμή t₂;  Ποια χρονική στιγμή το αυτοκίνητο περνά από τη θέση x₂=4m.

Μονάδες 20+15+20+45=100

Μέση και στιγμιαία ταχύτητα.

Δύο εφαρμογές για εξάσκηση.

1) Ένα σώμα κινείται ευθύγραμμα και στο διάγραμμα δίνεται η θέση του  σε συνάρτηση με το χρόνο.

i) Ποια η ταχύτητα του σώματος τις χρονικές στιγμές:

α)  t₁= 1s       β)       t₂=2s   γ) t₃=3,5s  και t₄=5s.

υ₁=………    υ₂= …………..υ₃=………….υ₄= ………

ii)  Να βρεθεί η μέση ταχύτητα του σώματος:

α) από 0-4s              β) από 0-6s.

iii) Να βρεθεί η μετατόπιση και το διάστημα που  διένυσε το σώμα στο χρονικό διάστημα  από 0-6s.

2)  Ένα σώμα κινείται ευθύγραμμα και στο διάγραμμα δίνεται η ταχύτητά του σε συνάρτηση με το χρόνο.

i) Ποια η ταχύτητα του σώματος τις χρονικές στιγμές:

α) t₁=0s β) t₂=4s        γ) t₃=8s                  δ) t₄=10s     ε) t₅=20s

υ₁=………    υ₂= …………..υ₃=………….υ₄= ……… υ₅= …..

ii) Να βρεθεί η μέση ταχύτητα του σώματος στα χρονικά διαστήματα:

α) Από  0-3s              β) Από 5s-15s           γ) από 0-10s

δ) Από 10s-25s          δ) Από 0-25s

Απάντηση:

Θέματα Εξετάσεων Φυσικής Α΄Λυκείου 2011

Ένα παιδί ασκώντας σε ένα βιβλίο βάρους 2Ν μια οριζόντια δύναμη F=4Ν, το υποχρεώνει να παραμένει ακίνητο σε επαφή με κατακόρυφο τοίχο, όπως στο σχήμα.

i)  Ο τοίχος είναι λείος.

ii) Στο βιβλίο ασκείται δύναμη τριβής οριζόντια με μέτρο ίσο με 4Ν.

iii) Στο βιβλίο ασκείται κατακόρυφη τριβή με φορά προς τα πάνω και μέτρο ίσο με 2Ν.

 Να επιλέξτε την σωστή πρόταση, δικαιολογώντας αναλυτικά την επιλογή σας, σχεδιάζοντας παράλληλα και όλες τις δυνάμεις που  ασκούνται στο βιβλίο.

Δείτε όλα τα θέματα από εδώ ή εδώ.